前面,我们介绍了Trie树结构,它的实现简单但空间效率低。如果要支持26个英文字母,每个节点就要保存26个指针,假若我们还要支持国际字符、标点符号、区分大小写,内存用量就会急剧上升,以至于不可行。
由于节点数组中保存的空指针占用了太多内存,我们遇到的困难与此有关,因此可以考虑改用其他数据结构去代替,比如用hash map。然而,管理成千上万个hash map肯定也不是什么好主意,而且它使数据的相对顺序信息丢失,所以我们还是去看看另一种更好解法吧——Ternary Tree。
接下来,我们将介绍三叉搜索树,它结合字典树的时间效率和二叉搜索树的空间效率优点。
Ternary Tree的实现
三叉搜索树使用了一种聪明的手段去解决Trie的内存问题(空的指针数组)。为了避免多余的指针占用内存,每个Trie节点不再用数组来表示,而是表示成“树中有树”。Trie节点里每个非空指针都会在三叉搜索树里得到属于它自己的节点。
接下来,我们将实现三叉搜索树的节点类,具体实现如下:
/// <summary>
/// The node type.
/// Indicates the word completed or not.
/// </summary>
public enum NodeType
{
COMPLETED,
UNCOMPLETED
};
/// <summary>
/// The tree node.
/// </summary>
public class Node
{
internal char Word { get; set; }
internal Node LeftChild, CenterChild, RightChild;
internal NodeType Type { get; set; }
public Node(char ch, NodeType type)
{
Word = ch;
Type = type;
}
}由于三叉搜索树包含三种类型的箭头。第一种箭头和Trie里的箭头是一样的,也就是图2里画成虚线的向下的箭头。沿着向下箭头行进,就意味着“匹配上”了箭头起始端的字符。如果当前字符少于节点中的字符,会沿着节点向左查找,反之向右查找。
接下来,我们将定义Ternary Tree类型,并且添加Insert(),Find()和FindSimilar()方法。
/// <summary>
/// The ternary tree.
/// </summary>
public class TernaryTree
{
private Node _root;
////private string _prefix;
private HashSet<string> _hashSet;
/// <summary>
/// Inserts the word into the tree.
/// </summary>
/// <param name="s">The word need to insert.</param>
/// <param name="index">The index of the word.</param>
/// <param name="node">The tree node.</param>
private void Insert(string s, int index, ref Node node)
{
if (null == node)
{
node = new Node(s[index], NodeType.UNCOMPLETED);
}
if (s[index] < node.Word)
{
Node leftChild = node.LeftChild;
this.Insert(s, index, ref node.LeftChild);
}
else if (s[index] > node.Word)
{
Node rightChild = node.RightChild;
this.Insert(s, index, ref node.RightChild);
}
else
{
if (index + 1 == s.Length)
{
node.Type = NodeType.COMPLETED;
}
else
{
Node centerChild = node.CenterChild;
this.Insert(s, index + 1, ref node.CenterChild);
}
}
}
/// <summary>
/// Inserts the word into the tree.
/// </summary>
/// <param name="s">The word need to insert.</param>
public void Insert(string s)
{
if (string.IsNullOrEmpty(s))
{
throw new ArgumentException("s");
}
Insert(s, 0, ref _root);
}
/// <summary>
/// Finds the specified world.
/// </summary>
/// <param name="s">The specified world</param>
/// <returns>The corresponding tree node.</returns>
public Node Find(string s)
{
if (string.IsNullOrEmpty(s))
{
throw new ArgumentException("s");
}
int pos = 0;
Node node = _root;
_hashSet = new HashSet<string>();
while (node != null)
{
if (s[pos] < node.Word)
{
node = node.LeftChild;
}
else if (s[pos] > node.Word)
{
node = node.RightChild;
}
else
{
if (++pos == s.Length)
{
_hashSet.Add(s);
return node.CenterChild;
}
node = node.CenterChild;
}
}
return null;
}
/// <summary>
/// Get the world by dfs.
/// </summary>
/// <param name="prefix">The prefix of world.</param>
/// <param name="node">The tree node.</param>
private void DFS(string prefix, Node node)
{
if (node != null)
{
if (NodeType.COMPLETED == node.Type)
{
_hashSet.Add(prefix + node.Word);
}
DFS(prefix, node.LeftChild);
DFS(prefix + node.Word, node.CenterChild);
DFS(prefix, node.RightChild);
}
}
/// <summary>
/// Finds the similar world.
/// </summary>
/// <param name="s">The prefix of the world.</param>
/// <returns>The world has the same prefix.</returns>
public HashSet<string> FindSimilar(string s)
{
Node node = this.Find(s);
this.DFS(s, node);
return _hashSet;
}
}和Trie类似,我们在TernaryTree 类中,定义了Insert(),Find()和FindSimilar()方法,它包含两个字段分别是:_root和_hashSet,_root用来保存Trie树的根节点,我们使用_hashSet保存前缀匹配的所有单词。
由于三叉搜索树每个节点只有三个叉,所以我们在进行节点插入操作时,只需判断插入的字符与当前节点的关系(少于,等于或大于)插入到相应的节点就OK了。
我们使用之前的例子,把字符串AB,ABBA,ABCD和BCD插入到三叉搜索树中,首先往树中插入了字符串AB,接着我们插入字符串ABCD,由于ABCD与AB有相同的前缀AB,所以C节点都是存储到B的CenterChild中,D存储到C的CenterChild中;当插入ABBA时,由于ABBA与AB有相同的前缀AB,而B字符少于字符C,所以B存储到C的LeftChild中;当插入BCD时,由于字符B大于字符A,所以B存储到C的RightChild中。
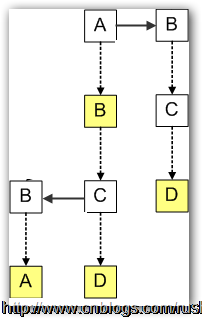
图4三叉搜索树
我们注意到插入字符串的顺序会影响三叉搜索树的结构,为了取得最佳性能,字符串应该以随机的顺序插入到三叉树搜索树中,尤其不应该按字母顺序插入,否则对应于单个Trie
节点的子树会退化成链表,极大地增加查找成本。当然我们还可以采用一些方法来实现自平衡的三叉树。
由于树是否平衡取决于单词的读入顺序,如果按排序后的顺序插入,则该方式生成的树是最不平衡的。单词的读入顺序对于创建平衡的三叉搜索树很重要,所以我们通过选择一个排序后数据集合的中间值,并把它作为开始节点,通过不断折半插入中间值,我们就可以创建一棵平衡的三叉树。我们将通过方法BalancedData()实现数据折半插入,具体实现如下:
/// <summary>
/// Balances the ternary tree input data.
/// </summary>
/// <param name="file">The file saves balanced data.</param>
/// <param name="orderList">The order data list.</param>
/// <param name="offSet">The offset.</param>
/// <param name="len">The length of data list.</param>
public void BalancedData(StreamWriter file, IList<KeyValuePair<int, string>> orderList, int offSet, int len)
{
if (len < 1)
{
return;
}
int midLen = len >> 1;
// Write balanced data into file.
file.WriteLine(orderList[midLen + offSet].Key + " " + orderList[midLen + offSet].Value);
BalancedData(file, orderList, offSet, midLen);
BalancedData(file, orderList, offSet + midLen + 1, len - midLen - 1);
}上面,我们定义了方法BalancedData(),它包含四个参数分别是:file,orderList,offSet和len。File写入平衡排序后的数据到文本文件。orderList按顺序排序后的数据。offSet偏移量。Len插入的数据量。
同样我们创建一棵三叉搜索树,然后把两千个英语单词插入到三叉搜索树中,最后我们查找前缀为“ab”的所有单词包括前缀本身。
public class Program
{
public static void Main()
{
// Creates a file object.
var file = File.ReadAllLines(Environment.CurrentDirectory + "//1.txt");
// Creates a trie tree object.
var ternaryTree = new TernaryTree();
var dictionary = new Dictionary<int, string>();
foreach (var item in file)
{
var sp = item.Split(new char[] { ' ' }, StringSplitOptions.RemoveEmptyEntries);
ternaryTree.Insert(sp.LastOrDefault().ToLower());
}
Stopwatch watch = Stopwatch.StartNew();
// Gets words have the same prefix.
var similarWords = ternaryTree.FindSimilar("ab");
foreach (var similarWord in similarWords)
{
Console.WriteLine("Similar word: {0}", similarWord);
}
watch.Stop();
Console.WriteLine("Time consumes: {0} ms", watch.ElapsedMilliseconds);
Console.WriteLine("Similar word: {0}", similarWords.Count);
Console.Read();
}
}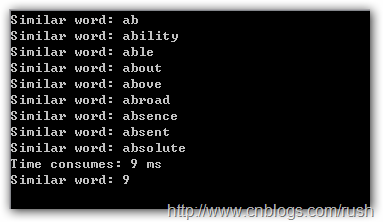
图5匹配结果
我们在1.txt文本文件中通过正则表达式(^:z ab+)查找前缀为ab的所有单词,刚好就是上面9个单词。
本文导航
- 第1页: 首页
- 第2页: Trie树的实现
- 第3页: Ternary Tree的定义和实现
- 第4页: Ternary Tree的应用


 喜欢
喜欢  顶
顶 难过
难过 囧
囧 围观
围观 无聊
无聊